Insight into the Fourier analysis
- Prayoga Institute
- Apr 19, 2022
- 8 min read
Updated: Apr 24, 2023
Dr B. Lakshmi
Researcher, Department of Mathematics, Prayoga, Bengaluru
Albert Einstein was exactly right in making a profound statement that some of the most abstract pure mathematics involved in the theory of Fourier analysis had successfully been used in many fields of science and technology.
“pure mathematics enables us to discover the concepts and laws connecting them, which gives us the key to the understanding of the phenomena of nature’"
As we all know, technology has revolutionized the world, and we are all immensely reliant on it in order to live our daily lives. Today’s wireless communication systems, whether they are 4G or 5G, audio, video, tablets, and images, including JPEG and MP3, all depend on the transmission of signals. These may be analog signals or digital signals. These signals will be flying back and forth every minute of every day. Have you ever wondered how your wireless phone receives text messages, images, and videos? .How do billions of devices connect and share data all over the world? All these modern technological advancements are based on the signal analysis or signal processing, which works on the main principle of Fourier analysis and its ramification. Even though this modern technology is not the invention of just one person, if we would like to thank someone in particular for our modern digital life, it is Jean-Baptist Joseph Fourier.
An over view of Joseph Fourier’s life

Fig.1: French mathematician Jean Baptiste Joseph Fourier (1768 - 1830)
Jean-Baptist Joseph Fourier was born on 21 March1768 in an ancient town of Auxerre in France. When he was 10 years old both his parents died. He began his education in the Pallais elementary school, where he studied Latin and French. Even though he was good at both the languages, his mathematics and mechanics abilities were exceptional. He had completed a thorough study of six volumes of Etienne Be’zout’s (French mathematician who is best known for his theorem on the number of solutions of polynomial equations) course in Mathematics at the age of thirteen. At a very young age, Joseph presented a research paper on algebraic equations at the Acade´mie Royale des Sciences. Later in 1794 he was chosen to study at the E’cole Normale in Paris which was later established as a model school for teachers' training in France. He enrolled in this training institution and had the unique opportunity to meet most prominent French mathematicians at that time J. L. Lagrange, P. S. Laplace, and Gaspard Monge.
In 1798, Fourier was selected to join Napoleon Bonaparte’s Egyptian expedition as scientific advisor. Later in 1799 when Napoleon returned to Paris and became the Emperor of France. Fourier also came back to Paris to resume his position as Professor of Analysis at the E´colePolytechnique.
During this time his Mathematical and scientific work reached its peak. He had developed an intense interest in heat energy and used to keep his home unpleasantly worm and wore thick heavy coats. This eccentricity enabled him to achieve significant development in his theory of Heat flow. He applied mathematical techniques, on his observations and wrote a memoir entitled “On the propagation to heat in solid bodies”. He also proposed the idea that “any function whether continues or discontinuous could be written as an infinite sum the Sine and Cosine functions” which later became “Fourier series”. He presented his memoir to the Paris institute in 1807 and also to a committee that comprised of Mathematicians like Lagrange, Gaspard Monge, Lacroix and Laplace. Lagrange and Laplace both challenged his idea and later in 1892 the German mathematician Peter Gustav Dirichlet actually managed to demonstrate Fourier’s ideas and was able to lay down the conditions under which the theory works. This became the foundation of what would be known as Fourier transforms.
His discoveries will be valuable to many areas particularly to electrical field. His interest was in heat diffusion made him to discover that the atmosphere gases, their concentration and their nature affects the temperature of the earth this notion is now regarded as a “Green house effect”.
Periodic functions and Fourier series
In the early eighteenth century, C. Maclaurin and B. Taylor developed the power series extension of trigonometric and exponential functions. However, these mathematical expressions would not explode the concept of periodicity, which can be found in many physical phenomena such as string vibrations, voltage and currents in electrical networks, electromagnetic waves, and the movement of pendulums, etc. It was Joseph Fourier who gave us the mathematical tool called the Fourier series to describe the physical phenomena which are periodic in nature. The word periodic means any phenomenon that involves regular, repetitive behavior. The simplest examples are circular motion at constant velocity, the position of a planet in it orbit revolving around the sun is a periodic function of time, the arrangement of molecules in crystals exhibits a periodic structure. Even a heart rate is typically periodic over a short time scales in certain conditions.
Mathematically a Periodic function is a function that repeats its value at regular intervals. So any function f(t) is said to be a periodic function of period T if it satisfies the relation f(t + T)=f(t) for all real values of t. The trigonometric functions like sint, cost are all periodic functions of period 2π. As they repeat at intervals of 2π radians and tant ,cott are periodic functions of period π. That is sin(t + 2π)=sin t and cos(t + 2π)=cos t.

Fig.2 : Periodic Sine and Cosine waves
According to Fourier “Any periodic functions or signals can be represented by an infinite sum of sine or cosine functions of different frequencies” known as Fourier series. Since signals are periodic in nature they can be interpreted in terms of frequencies, thus can be rewritten as a sum of many sine and cosine signals. This makes the signal easier to understand and analyze because its components can be studied in a better way. So, Fourier series of decomposing the signal or any periodic function (mathematically) into sine and cosine waves of different frequencies became the starting point for finding the steady-state response to periodic excitations of electric circuits.
Let us understand this mathematically, if f(x) is any periodic function or signal of period T=2π defined in the interval (α, α+2π) then the Fourier series of f(x) can be written as,

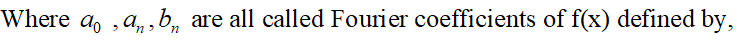


Let us understand this analysis by taking an Example of how a Square wave signal can be decomposed as a sum of odd harmonics of sinusoids,

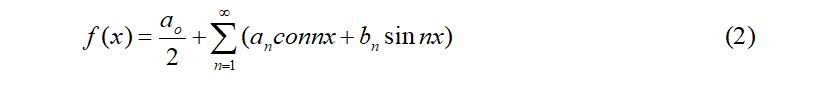
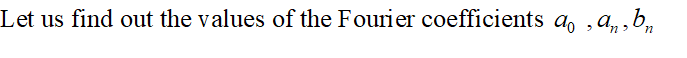



When you feed a wave (Fig.3.Square wave) into the Fourier series, it spits out the ingredients of that wave in the form of a number of sine and cosine waves that, when combined together, rebuild the wave (Fig.4).

Fig.3: Decomposition of Square wave in to number of sine waves
Source: http://tex.stackexchange.com/

Fig.4: Number of sine terms added up to produce a square wave
Isn't it amazing that our ears perform Fourier series automatically when we hear a sound?
In our ears, there are thousands of hairs of various lengths that vibrate at different frequencies. The hairs in the ear help the brain to break down the complex sound waves into separate frequencies. Rather than processing the entire sound wave, the brain can analyze the same data by analyzing individual sinusoids. As a result, humans can discern between sounds of varying pitch.
Fourier transforms
Fourier transforms is the extension of the Fourier series can be applied to of non-periodic signals. The Fourier transform of any function f(x) is defined as,

Inverse Fourier transform is
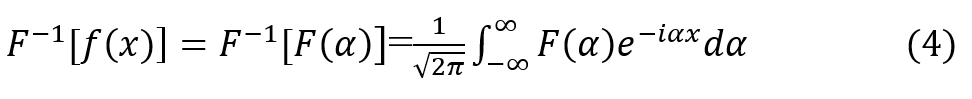
Where α is any non-zero real parameter.
When we take Fourier transforms of any signal f(x), we can move it from the time domain to the frequency domain as a sum of several sinusoids of different frequencies. That is, a step function in the time domain becomes a sync function in the frequency domain.

Fig 5: Transformation from time domain to frequency domain
Why do we need transformation from time domain to frequency domain?
The number of times an event has occurred during the total period of observation is known as frequency. So, rather than observing every modification that occurs in the time domain, analyzing the frequency domain is considerably easier since we can identify the relevant points in the overall interval. If we have a signal in the time domain, we must convert this to frequency domain using Fourier transforms is required to determine the changes after passage through the devices. Later, using Inverse Fourier transforms, this signal can be turned into a time domain signal to see the changes.
This notion is employed in image processing. When we apply the Fourier transform to an image, we convert it from its 'spatial domain' (time domain) to a 'frequency domain', which is the image expressed in terms of its colour and brightness variations over time.
We all know that radio, television and cell phones transmit information through electromagnetic waves. The multiple sources in these applications may be broadcasted in the same geographic region at the same time. But, instead of hearing a cacophony of all the transmissions combined, we may tune in to a certain radio station, different TV programs or may tune in to a person with whom we are interacting. The answer is that different transmissions agree to use different frequencies. Thus, even though all the signals are muddled up together in the time domain, if we convert them in to frequency domain, these signals will be distinct in frequency domain. It is straight-forward to separate the signals and “tune in” to the frequency we are interested in.
It's fascinating that the MP3 format compresses wave files using a variant of Fourier's technique. An MP3 is a format for breaking down a song into smaller chunks. Fourier's trick breaks down each audio segment into its component notes, which are then stored in place of the original wave. The Fourier transform also informs you how much each note contributes to the music, allowing you to determine which notes are most important. Because the really high notes aren't as vital, MP3s eliminate them, resulting in increased data compression.
The Fourier transform is also an important tool used in MRI and CT scans. In MRI, we deliver pulses to the region of interest at precise times, for a specific duration, and at a specific angle of incidence, and then collect the data that we need. This space which contains array of numbers or data representing spatial frequencies in the MR image is called the k-space. The final image that is used for diagnostic purposes is obtained by applying Fourier transforms.
In his description of the relationship between pure mathematics and applied mathematics Albert Einstein says ‘pure mathematics enables us to discover the concepts and laws connecting them, which gives us the key to the understanding of the phenomena of nature’. He was exactly right in making such a profound statement that some of the most abstract pure mathematics involved in the theory of Fourier analysis had successfully been used in many fields of science and technology, including vibration analysis, optics, acoustics, circuit analysis, image processing, signal processing and filtering, quantum mechanics, econometrics, shell theory, to develop the analytical theory of the flow of heat in solid bodies of different geometric configurations, in geology to distinguish between natural seismic events and nuclear test explosions as they generate different frequency spectra, and many more.
Fourier’s contribution to the field of mathematical science and its applications to modern technology are enormous. We must remember and commemorate Fourier for his splendid scientific achievements.
References
[1] Lokenath Debnath - A short biography of Joseph Fourier and historical development of Fourier series and Fourier transforms, International journal of Mathematical education in Science and Technology, vol43, issue5, p589612.https://doi.org/10.1080/0020739X.2011.633712
[2] S. Thangavelu - Fourier series The Mathematics of Periodic Phenomena. Resonance –Journal of Science Education.Vol1, issue10, p 44-55.
[3] Steven W. Smith - The scientist and Engineer’s guide to Digital signal Processing, second edition, California Technical Publishing,1999.
_PNG.png)




Comments